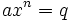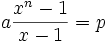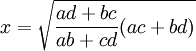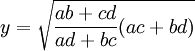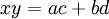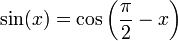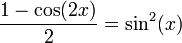RAMANUJAN
- He was born on 22naof December 1887 in a small village of Tanjore district, Madras.He failed in English in Intermediate, so his formal studies were stopped but his self-study of mathematics continued.
- He sent a set of 120 theorems to Professor Hardy of Cambridge. As a result he invited Ramanujan to England.
- Ramanujan showed that any big number can be written as sum of not more than four prime numbers.
- He showed that how to divide the number into two or more squares or cubes.
- when Mr Litlewood came to see Ramanujan in taxi number 1729, Ramanujan said that 1729 is the smallest number which can be written in the form of sum of cubes of two numbers in two ways,i.e. 1729 = 93 + 103 = 13 + 123since then the number 1729 is called Ramanujan’s number.
- In the third century B.C, Archimedes noted that the ratio of circumference of a circle to its diameter is constant. The ratio is now called ‘pi ( Π )’ (the 16th letter in the Greek alphabet series)
- The largest numbers the Greeks and the Romans used were 106 whereas Hindus used numbers as big as 1053 with specific names as early as 5000 B.C. during the Vedic period.
ARYABHATTA
- Aryabhatta was born in 476A.D in Kusumpur, India.
- He was the first person to say that Earth is spherical and it revolves around the sun.
- He gave the formula (a + b)2 = a2 + b2 + 2ab
- He taught the method of solving the following problems:
14 + 24 + 34 + 44 + 54 + …………+ n4 = n(n+1) (2n+1) (3n2+3n-1)/30
BRAHMA GUPTA
- Brahma Gupta was born in 598A.D in Pakistan.
- He gave four methods of multiplication.
- He gave the following formula, used in G.P series
a + ar + ar2 + ar3 +……….. + arn-1 = (arn-1) ÷ (r – 1)
- He gave the following formulae :
Area of a cyclic quadrilateral with side a, b, c, d= √(s -a)(s- b)(s -c)(s- d)
where 2s = a + b + c + d
Length of its diagonals =
SHAKUNTALA DEVI
- She was born in 1939
- In 1980, she gave the product of two, thirteen digit numbers within 28 seconds, many countries have invited her to demonstrate her extraordinary talent.
- In Dallas she competed with a computer to see who give the cube root of 188138517 faster, she won. At university of USA she was asked to give the 23rdroot of9167486769200391580986609275853801624831066801443086224071265164279346570408670965932792057674808067900227830163549248523803357453169351119035965775473400756818688305620821016129132845564895780158806771.She answered in 50seconds. The answer is 546372891. It took a UNIVAC 1108 computer, full one minute (10 seconds more) to confirm that she was right after it was fed with 13000 instructions.Now she is known to be Human Computer.
BHASKARACHARYA
- He was born in a village of Mysore district.
- He was the first to give that any number divided by 0 gives infinity (00).
- He has written a lot about zero, surds, permutation and combination.
- He wrote, “The hundredth part of the circumference of a circle seems to be straight. Our earth is a big sphere and that’s why it appears to be flat.”
- He gave the formulae like sin(A ± B) = sinA.cosB ± cosA.sinB
Mahavira
Mahavira was a 9th-century Indian mathematician from Gulbarga who asserted that the square root of a negative number did not exist. He gave the sum of a series whose terms are squares of an arithmetical progression and empirical rules for area and perimeter of an ellipse. He was patronised by the great Rashtrakuta king Amoghavarsha. Mahavira was the author of Ganit Saar Sangraha. He separated Astrology from Mathematics. He expounded on the same subjects on which Aryabhata and Brahmagupta contended, but he expressed them more clearly. He is highly respected among Indian Mathematicians, because of his establishment of terminology for concepts such as equilateral, and isosceles triangle; rhombus; circle and semicircle. Mahavira’s eminence spread in all South India and his books proved inspirational to other Mathematicians in Southern India.
Higher-order equations
Mahavira solved higher order equations of n degree of the forms:
And
Formula for cyclic quadrilateral
Mahavira expressed characteristics of a cyclic quadrilateral, like Brahmagupta did previously. He also established equations for the sides and diagonal of Cyclic Quadrilateral.
If sides of Cyclic Quadrilateral are a,b,c,d and its diagonals are x and y while
And
Then,
Pythagoras
[Samos, 582 – 500 BC]
Like Thales, Pythagoras is rather known for mathematics than for philosophy. Anyone who can recall math classes will remember the first lessons of plane geometry that usually start with the Pythagorean theorem about right-angled triangles: a²+b²=c². In spite of its name, the Pythagorean theorem was not discovered by Pythagoras. The earliest known formulation of the theorem was written down by the Indian mathematician BaudhÄyana in 800BC. The principle was also known to the earlier Egyptian and the Babylonian master builders. However, Pythagoras may have proved the theorem and popularised it in the Greek world. With it, his name and his philosophy have survived the turbulences of history.
His immediate followers were strongly influenced by him, and even until today Pythagoras shines through the mist of ages as one of the brightest figures of early Greek antiquity. The Pythagorean theorem is often cited as the beginning of mathematics in Western culture, and ever since mathematics -the art of demonstrative and deductive reasoning- has had a profound influence on Western philosophy, which can be observed down to Russell and Wittgenstein.
Pythagoras’ influence found an expression in visual art and music as well, particularly in the renaissance and baroque epoch. The far-reaching imprint of his ideas is yet more impressive if we consider that he did not leave any original writings. Instead, all what is known about Pythagoras was handed down by generations of philosophers and historiographers, some of whom, like Heraclitus, opposed his views. In this light it is remarkable that Pythagoras’ teachings have survived relatively undistorted until the present day.
Pythagoras was a native of the island of Samos. During his early life, Samos was governed by the powerful, unscrupulous tyrant Polycrates. Pythagoras did not sympathise with his government and thus emigrated to Croton in Southern Italy. Like the ancient Greek cities in Ionia, Croton was a flourishing commercial city that lived from importing and exporting goods. Obviously it was in Croton where Pythagoras developed most of his important ideas and theories.
Pythagoras founded a society of disciples which has been very influential for some time. Men and women in the society were treated equally -an unusual thing at the time- and all property was held in common. Members of the society practised the master’s teachings, a religion the tenets of which included the transmigration of souls and the sinfulness of eating beans. Pythagoras’ followers had to obey strict religious orders where it was forbidden to eat beans, to touch white cocks, or to look into a mirror beside a light.
If all of this seems a bit odd, it might lead us to suspect that Pythagoras’ personality reflects the inseparable blend of genius and madness that we associate with many other great men. It is said that once Pythagoras was walking up a lane in Croton when he came by a dog being ill-treated. Seeing this he raised his voice: “Stop, don’t hit it! It is a soul of a friend. I knew it when I heard its voice.” Spirits, ghosts, souls, and transmigration were obviously things he believed in deeply.
There was an opposition -if not rivalry- in ancient Greece between the gods of the Olympus and the lesser gods of more primitive religions. Pythagoras, like no other, embodied the contradistinctions of the mystical and rational world, which is woven into his personality and philosophy. In his mind, numbers, spirits, souls, gods and the mystic connections between them formed one big picture. The following text tells the legend of his own existences:
“He was once born as Aethalides and was considered to be the son of Hermes. Hermes invited him to choose whatever he wanted, except immortality; so he asked that, alive and dead, he should remember what happened to him. Thus, in life he remembered everything, and when he died he retained the same memories. […] He remembered everything – how he first had been Aethalides, then Euphorbus, then Hermotimus, then Pyrrhus, the Delian fisherman. When Pyrrhus died, he became Pythagoras.” (Diogenes Laertius, Live of Philosophers, VIII 4-5)
“Pythagoras believed in metempsychosis and thought that eating meat was an abominable thing, saying that the souls of all animals enter different animals after death. He himself used to say that he remembered being, in Trojan times, Euphorbus, Panthus’ son who was killed by Menelaus. They say that once when he was staying at Argos he saw a shield from the spoils of Troy nailed up, and burst into tears. When the Argives asked him the reason for his emotion, he said that he himself had borne that shield at Troy when he was Euphorbus.
They did not believe him and judged him to be mad, but he said he would provide a true sign that it was indeed the case: on the inside of the shield there had been inscribed in archaic lettering EUPHORBUS. Because of the extraordinary nature of his claim they all urged that the shield be taken down – and it turned out that on the inside the inscription was found.” (Diogenes Laertius)
After Pythagoras introduced the idea of eternal recurrence into Greek thought, which was apparently motivated by his studies of earlier Egyptian scriptures, the idea soon became popular in Greece. It was Pythagoras’ ambition to reveal in his philosophy the validity and structure of a higher order, the basis of the divine order, for which souls return in a constant cycle.
This is how Pythagoras came to mathematics. It could be said that Pythagoras saw the study of mathematics as a purifier of the soul, just like he considered music as purifying. Pythagoras and his disciples connected music with mathematics and found that intervals between notes can be expressed in numerical terms. They discovered that the length of strings of a musical instrument correspond to these intervals and that they can be expressed in numbers. The ratio of the length of two strings with which two tones of an octave step are produced is 2:1.
Music was not the only field that Pythagoras considered worthy of study, in fact he saw numbers in everything. He was convinced that the divine principles of the universe, though imperceptible to the senses, can be expressed in terms of relationships of numbers. He therefore reasoned that the secrets of the cosmos are revealed by pure thought, through deduction and analytic reflection on the perceptible world.
This eventually led to the famous saying that “all things are numbers.” Pythagoras himself spoke of square numbers and cubic numbers, and we still use these terms, but he also spoke of oblong, triangular, and spherical numbers. He associated numbers with form, relating arithmetic to geometry. His greatest contribution, the proposition about right-angled triangles, sprang from this line of thought:
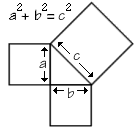
Let us suppose each side is an inch long; then how long is the hypotenuse? Let us suppose its length is m/n inches. Then m²/n²=2. If m and n have a common factor, divide it out, then either m or n must be odd. Now m²=2n², therefore m² is even, therefore m is even, therefore n is odd. Suppose m=2p. Then 4p²=2n², therefore n²=2p² and therefore n is even, contra hyp. Therefore no fraction m/n will measure the hypotenuse. The above proof is substantially that in Euclid, Book X.” (Bertrand Russell, History of Western Philosophy)
This shows how Pythagoras’ formulation immediately led to a new mathematical problem, namely that of incommensurables. At his time the concept of irrational numbers was not known and it is uncertain how Pythagoras dealt with the problem. We may surmise that he was not too concerned about it. His religion, in absence of theological explanations, had found a way to blend the “mystery of the divine” with common-sense rational thought.
From Pythagoras we observe that an answer to a problem in science may give raise to new questions. For each door we open, we find another closed door behind it. Eventually these doors will be also be opened and reveal answers in a new dimension of thought. A sprawling tree of progressively complex knowledge evolves in such manner. This Hegelian recursion, which is in fact a characteristic of scientific thought, may or may not have been obvious to Pythagoras. In either way he stands at the beginning of it.
- Aryabhata I
Aryabhata (476-550) wrote the Aryabhatiya. He described the important fundamental principles of mathematics in 332 shlokas. The treatise contained:
- Quadratic equations
- Trigonometry
- The value of π, correct to 4 decimal places.
Aryabhata also wrote the Arya Siddhanta, which is now lost. Aryabhata’s contributions include:
Trigonometry:
- Introduced the trigonometric functions.
- Defined the sine (jya) as the modern relationship between half an angle and half a chord.
- Defined the cosine (kojya).
- Defined the versine (ukramajya).
- Defined the inverse sine (otkram jya).
- Gave methods of calculating their approximate numerical values.
- Contains the earliest tables of sine, cosine and versine values, in 3.75° intervals from 0° to 90°, to 4 decimal places of accuracy.
- Contains the trigonometric formula sin (n + 1) x – sin nx = sin nx – sin (n – 1) x – (1/225)sin nx.
- Spherical trigonometry.
Arithmetic:
Algebra:
- Solutions of simultaneous quadratic equations.
- Whole number solutions of linear equations by a method equivalent to the modern method.
- General solution of the indeterminate linear equation .
Mathematical astronomy:
- Proposed for the first time, a heliocentric solar system with the planets spinning on their axes and following an elliptical orbit around the Sun.
- Accurate calculations for astronomical constants, such as the:
- Solar eclipse.
- Lunar eclipse.
- The formula for the sum of the cubes, which was an important step in the development of integral calculus.[60]
Calculus:
- Infinitesimals:
- In the course of developing a precise mapping of the lunar eclipse, Aryabhatta was obliged to introduce the concept of infinitesimals (tatkalika gati) to designate the near instantaneous motion of the moon.[61]
- Differential equations:
- He expressed the near instantaneous motion of the moon in the form of a basic differential equation.[61]
- Exponential function:
- He used the exponential function e in his differential equation of the near instantaneous motion of the moon.[61]
- Varahamihira
Varahamihira (505-587) produced the Pancha Siddhanta (The Five Astronomical Canons). He made important contributions to trigonometry, including sine and cosine tables to 4 decimal places of accuracy and the following formulas relating sine and cosine functions:
- sin2(x) + cos2(x) = 1
Niels Henrik Abel
Niels Henrik Abel (August 5, 1802 – April 6, 1829) was a noted Norwegian mathematician[1] who proved the impossibility of solving the quintic equation in radicals.
Carl Friedrich Gauss
Johann Carl Friedrich Gauss (pronounced /ˈɡaÊŠs/; German: Gauß listen (help·info), Latin: Carolus Fridericus Gauss) (30 April 1777 – 23 February 1855) was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics. Sometimes known as the Princeps mathematicorum[1] (Latin, “the Prince of Mathematicians” or “the foremost of mathematicians”) and “greatest mathematician since antiquity”, Gauss had a remarkable influence in many fields of mathematics and science and is ranked as one of history’s most influential mathematicians.[2] He referred to mathematics as “the queen of sciences.”[3]
Gauss was a child prodigy. There are many anecdotes pertaining to his precocity while a toddler, and he made his first ground-breaking mathematical discoveries while still a teenager. He completed Disquisitiones Arithmeticae, his magnum opus, in 1798 at the age of 21, though it would not be published until 1801. This work was fundamental in consolidating number theory as a discipline and has shaped the field to the present day.
Leonhard Euler
Leonhard Paul Euler (15 April 1707 – 18 September 1783) was a pioneering Swiss mathematician and physicist who spent most of his life in Russia and Germany. His surname is pronounced /ˈɔɪlÉ™r/ OY-lÉ™r in English and [ˈɔÊlÉ] in German; the common English pronunciation /ˈjuËlÉ™r/ EW-lÉ™r is incorrect.
Euler made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion of a mathematical function. He is also renowned for his work in mechanics, fluid dynamics, optics, and astronomy.
Euler is considered to be the preeminent mathematician of the 18th century and one of the greatest of all time. He is also one of the most prolific; his collected works fill 60–80 quarto volumes. A statement attributed to Pierre-Simon Laplace expresses Euler’s influence on mathematics: “Read Euler, read Euler, he is the master [i.e., teacher] of us all.”
Euler was featured on the sixth series of the Swiss 10-franc banknote and on numerous Swiss, German, and Russian postage stamps. The asteroid 2002 Euler was named in his honor. He is also commemorated by the Lutheran Church on their Calendar of Saints on 24 May – he was a devout Christian (and believer in biblical inerrancy) who wrote apologetics and argued forcefully against the prominent atheists of his time.
David Hilbert
David Hilbert (January 23, 1862 – February 14, 1943) was a German mathematician, recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. He discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of geometry. He also formulated the theory of Hilbert spaces one of the foundations of functional analysis.
Hilbert adopted and warmly defended Georg Cantor‘s set theory and transfinite numbers. A famous example of his leadership in mathematics is his 1900 presentation of a collection of problems that set the course for much of the mathematical research of the 20th century.
Hilbert and his students contributed significantly to establishing rigor and some tools to the mathematics used in modern physics. He is also known as one of the founders of proof theory, mathematical logic and the distinction between mathematics and metamathematics.
Bernhard Riemann
Georg Friedrich Bernhard Riemann (help·info) (German pronunciation: [ˈriËman]; September 17, 1826 – July 20, 1866) was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity.
Euclid