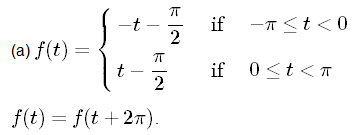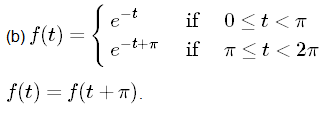Example 1 :
Determine the existence of odd or even harmonics for the following functions.
Answer :
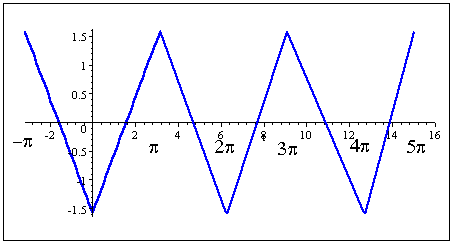
We can see from the graph that f(t+π)=−f(t).
For example, we notice that f(2)=0.4, approximately. If we now move π units to the right (or about 2+3.14=5.14), we see that the function value is
f(5.14)=−0.4.
That is, f(t+π)=−f(t).
This same behaviour will occur for any value of t that we choose.
So the Fourier Series will have odd harmonics.
This means that in our Fourier expansion we will only see terms like the following:
f(t)=a02+(a1 cos t+b1 sin t) + (a3 cos 3t+b3 sin 3t) + (a5 cos 5t+b5 sin 5t)+…
{Note: Don’t be confused with odd functions and odd harmonics. In this example, we have an even function (since it is symmetrical about the y-axis), but because the function has the property that f(t+π)=−f(t), then we know it has odd harmonics only.
The fact that it is an even function does not affect the nature of the harmonics and can be ignored.}
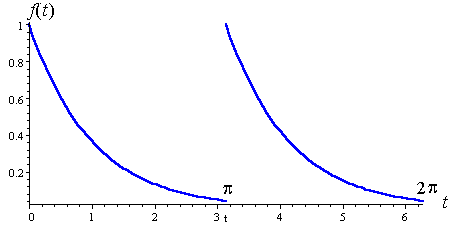
Answer:
The function is periodic with period π.
So, we conclude that the Fourier series will have even harmonics, and will be of the form: